Web 算数の範囲で解ける直角三角形の斜辺の長さは有名三角形に限られる。 HEFの辺の比を調べると3:4:5だから、HF=30cm PQ=30÷2=15cm 同様に JSRと JHFが相似。
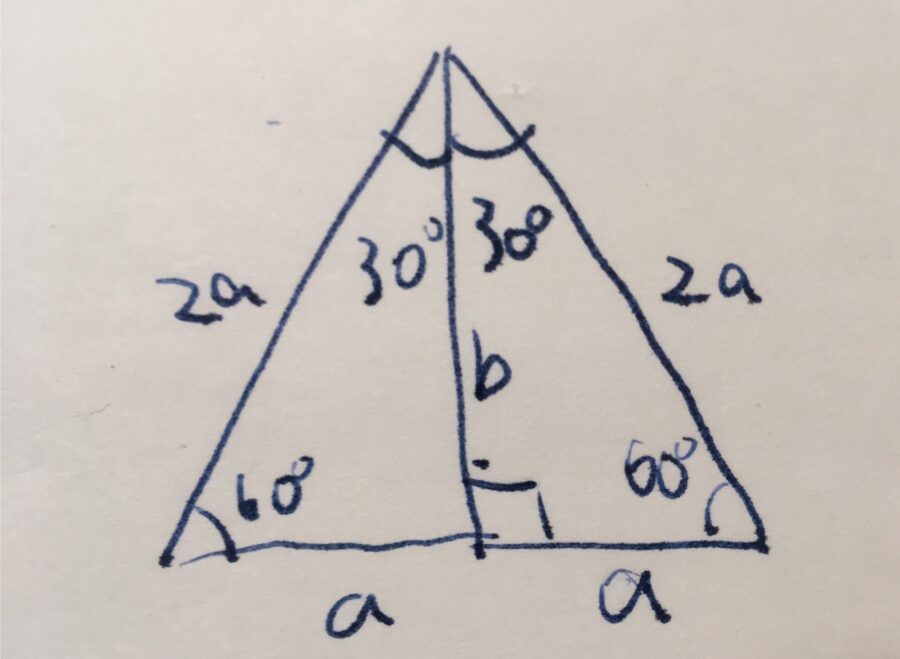
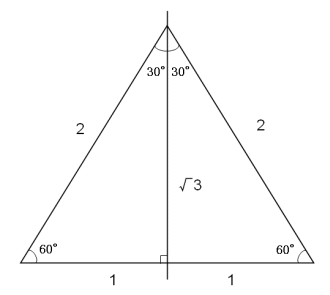
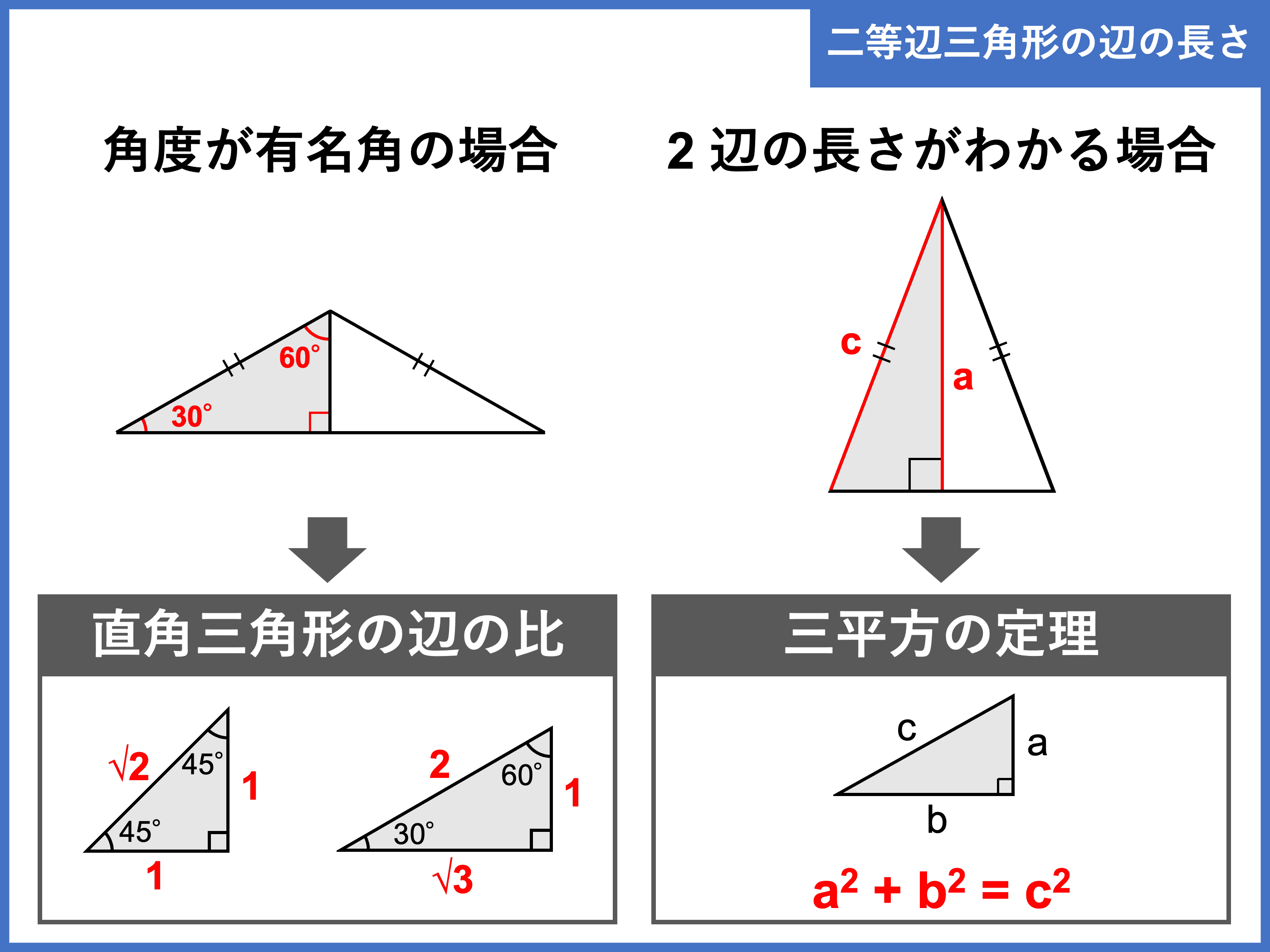
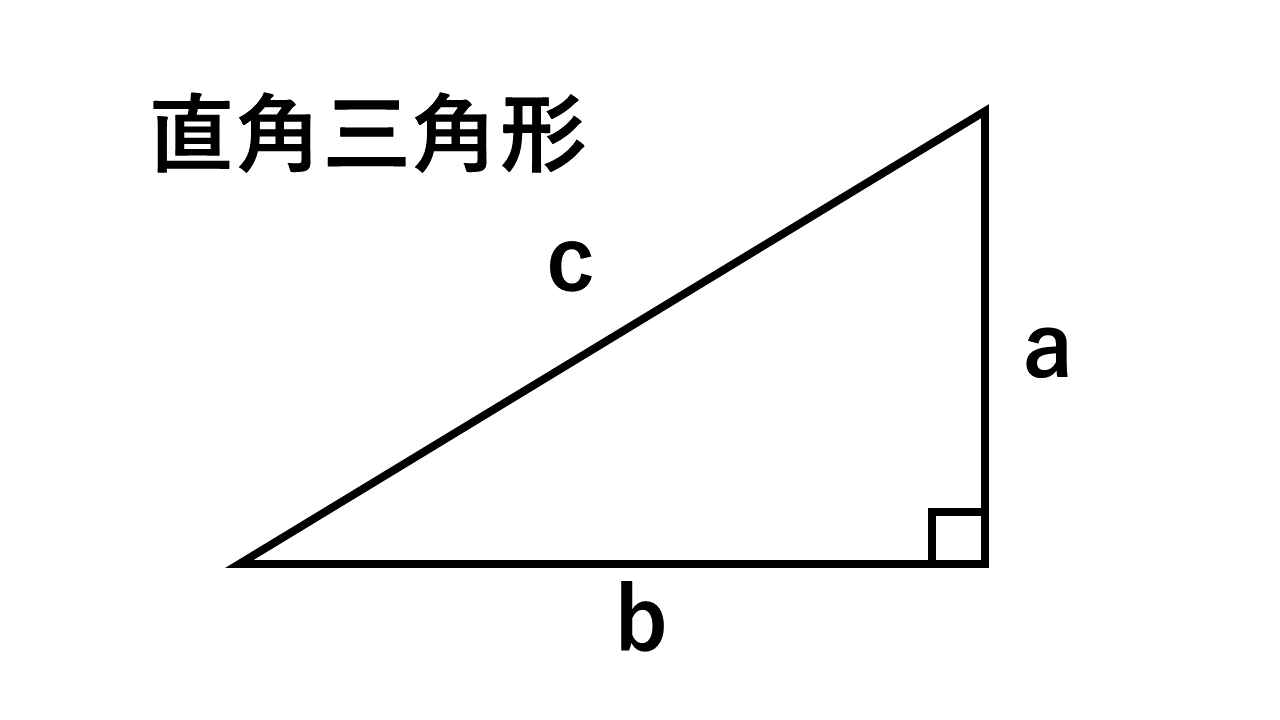
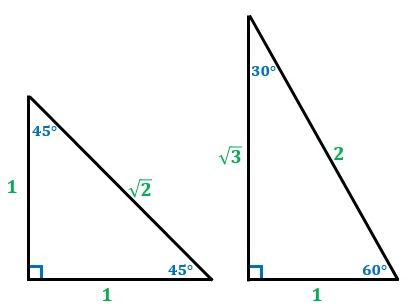
三角形 辺の比-Web辺の長さの比1:1:1 直角二等辺三角形です。 直角をはさむ2辺の長さは同じ です。 辺の長さの比1:1:√2 60°と30°の直角三角形です。 いちばん長い辺はいちばん短い辺の2倍の長Web次に、この直角三角形に注目して、辺の比を考えていきましょう。 今回は60°の直角三角形だから「\(12\sqrt{3}\)」であることがわかりますね。 ここでポイント! 円の半径についてス
三角形 辺の比のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 | 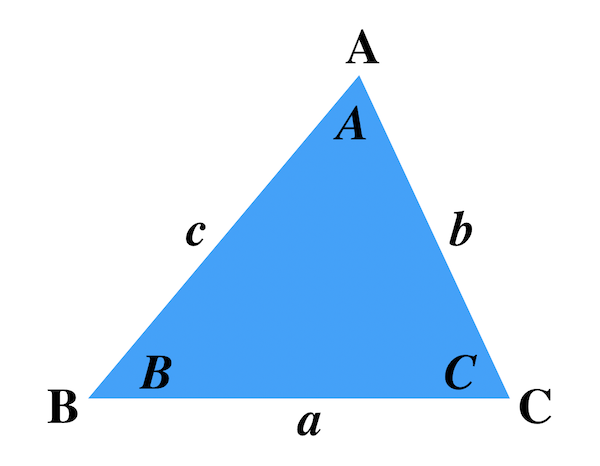 | 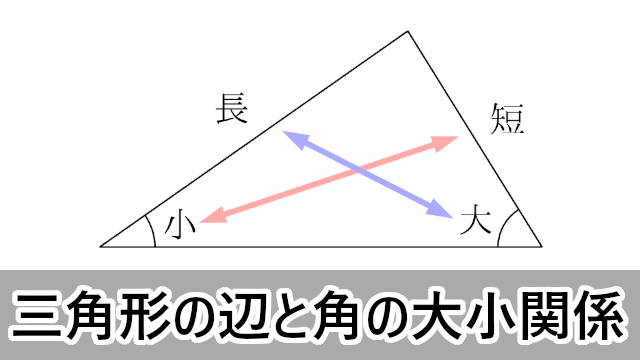 |
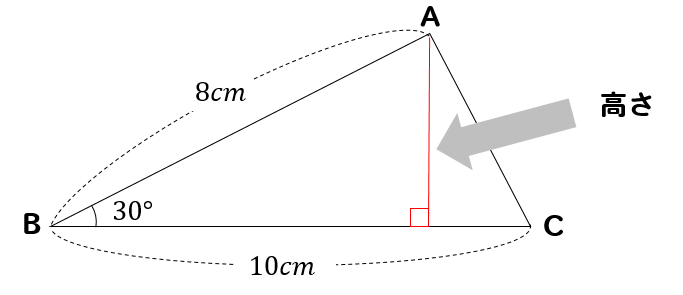 |  | |
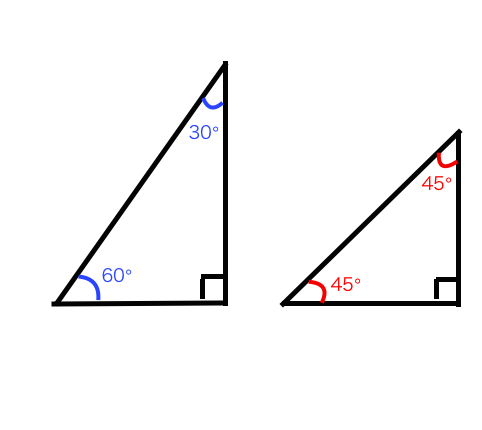 | ||
「三角形 辺の比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 | ||
「三角形 辺の比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 |  |  |
「三角形 辺の比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  |  |
「三角形 辺の比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  |  |
「三角形 辺の比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 |  | |
「三角形 辺の比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 | ||
「三角形 辺の比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 |  |  |
「三角形 辺の比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  |
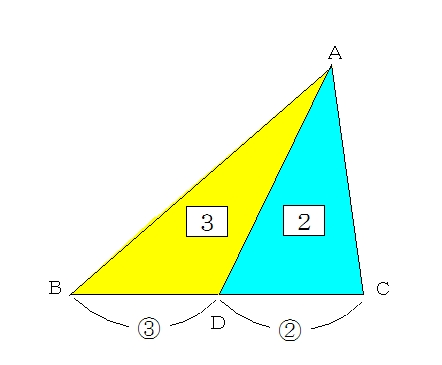
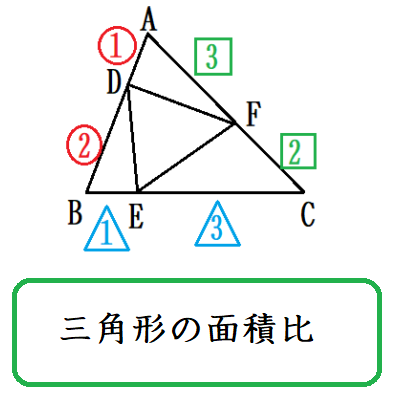
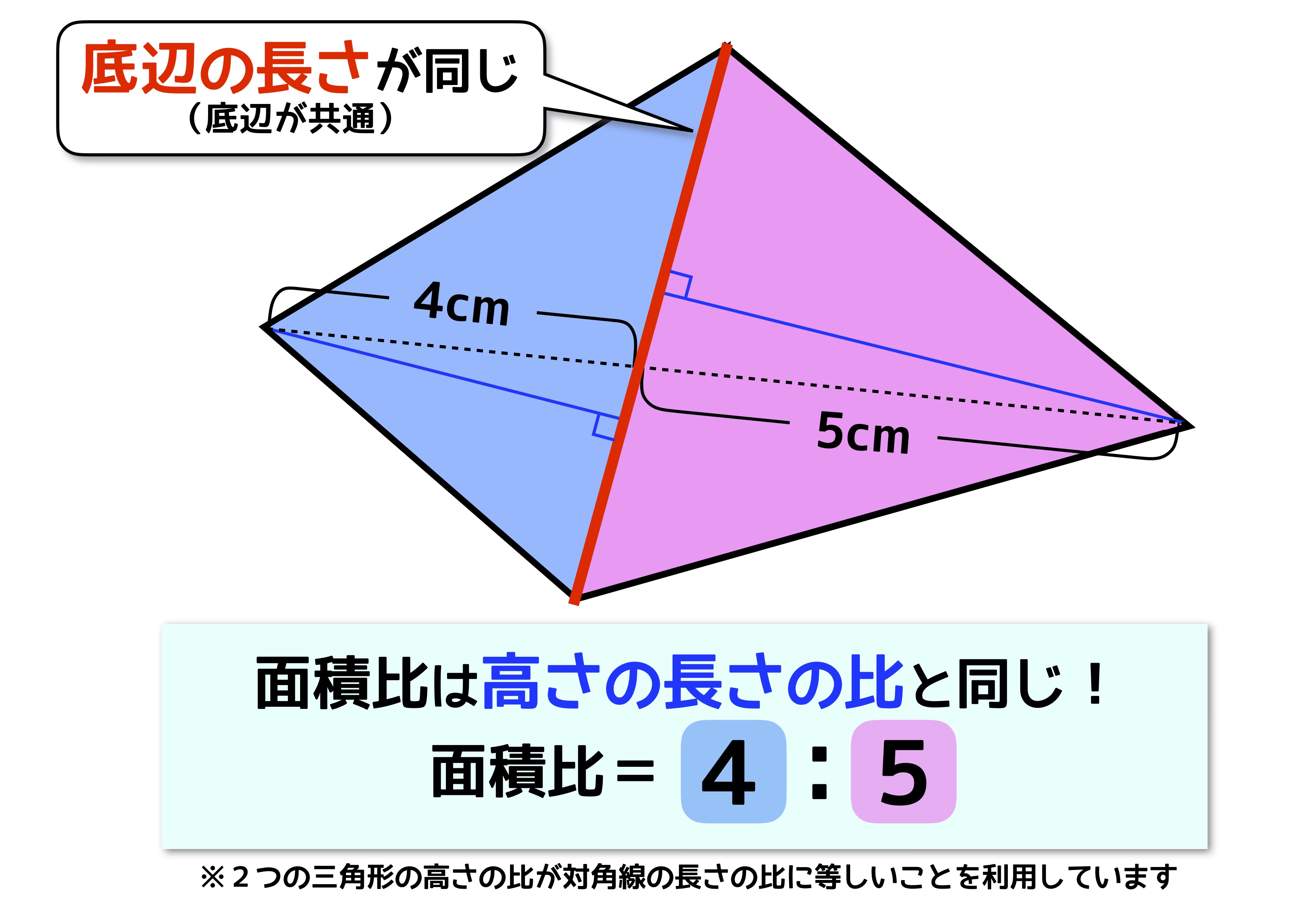
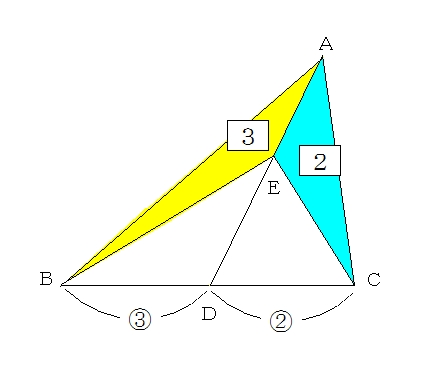
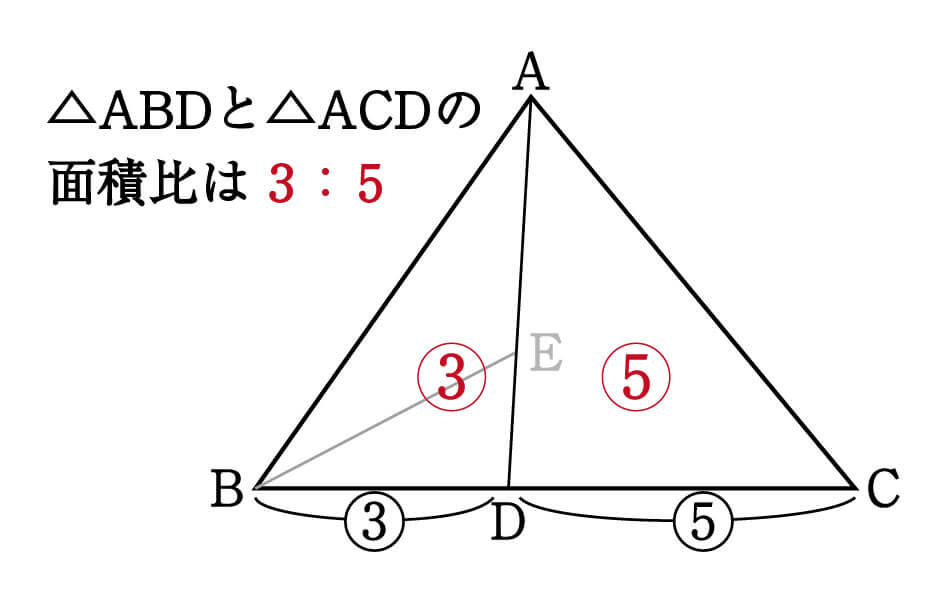
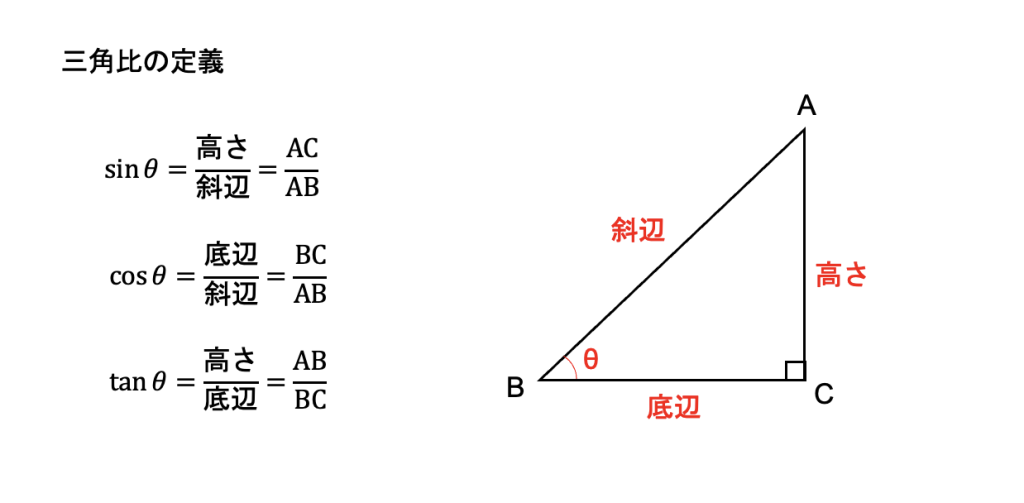
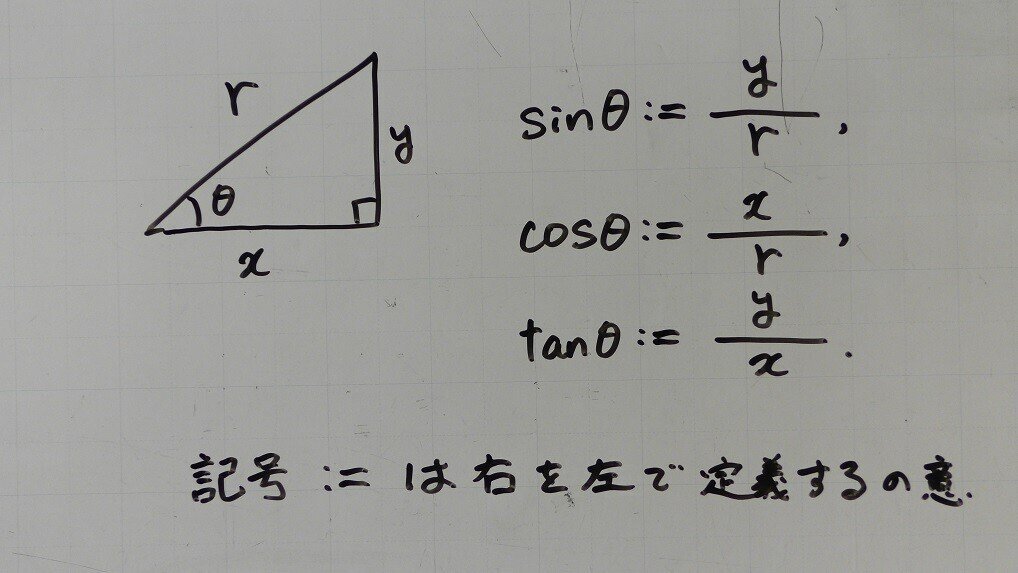
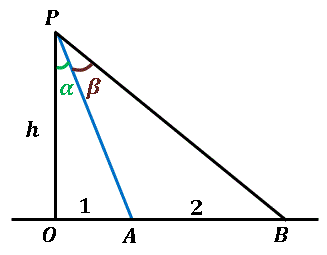
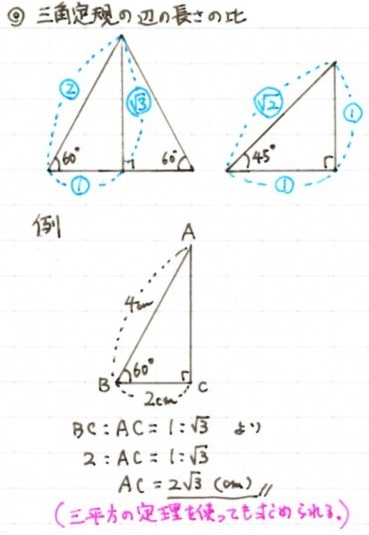
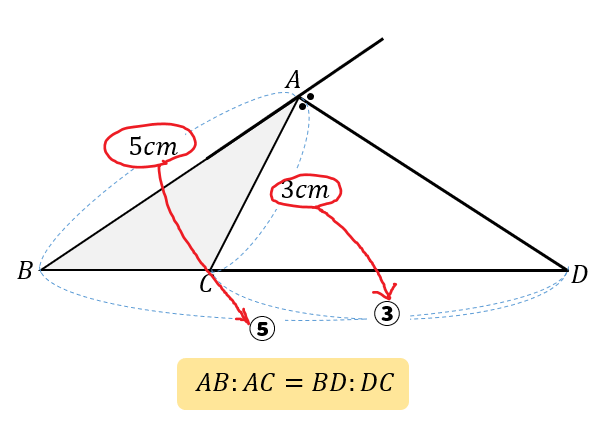
Web「一辺を共有する三角形の面積比は線分の比に変換できる」 と覚えておきましょう。 代表的な応用例としては, チェバの定理 の証明が挙げられます。 角を共有する三角形の面積比の公Web三角形の辺の長さを求めるときの三角比の値 下の図の x の値を求めよ。 これを解こうとすると,sin45°,sin60°という三角比が出てきました。 定義では,「直角三角形」だけで考える
Incoming Term: 三角形 辺の比, 三角形 辺の比 求め方, 三角形 辺の比 面積比, 三角形 辺の比 角度, 三角形 辺の比 公式, 三角形 辺の比 角度の比, 三角形 辺の比 高校, 三角形 辺の比と面積比, 三角形 辺の比 中学受験, 三角形 辺の比 二等分線,




0 件のコメント:
コメントを投稿